Model-Model Matematis

Model Linear

model linier digunakan dalam berbagai cara sesuai dengan konteksnya. Kejadian yang paling umum adalah sehubungan dengan model regresi dan istilah ini sering dianggap sama dengan model regresi linier . Namun, istilah ini juga digunakan dalam analisis deret waktu dengan makna yang berbeda. Dalam setiap kasus, penunjukan "linear" digunakan untuk mengidentifikasi subkelas model yang memungkinkan pengurangan substansial dalam kompleksitas teori statistik terkait.

Fungsi linear adalah fungsi yang dapat dinyatakan ke dalam bentuk

𝑓𝑥 = 𝑚+𝑐

Grafik fungsi tersebut berupa garis dengan gradien 𝑚 dan

memotong sumbu-y di 𝑐.

Polinomial

Dalam dunia matematika, polinomial atau suku banyak adalah pernyataan matematis yang berhubungan dengan jumlahan perkalian pangkat dalam satu atau lebih variabel dengan koefisien.

Bentuk umum dari suatu polinomial adalah sebagai berikut

koefisien konstan, dan pangkat tertinggi pada polinomial tersebut menandakan orde atau derajatnya, sehingga polinomial diatas memiliki derajat atau orde n.

dimana 𝑛 adalah bilangan bulat tidak negatif dan 𝑎0, 𝑎1, 𝑎2, …, 𝑎𝑛

adalah bilangan-bilangan real. Bilangan-bilangan 𝑎1, 𝑎2, …, 𝑎𝑛 yang

disebut koefisien dan 𝑎0 disebut konstanta.

Pembagian Polinomial

Pada umumnya, bentuk umum dari pembagian polinomial adalah

F(x) = P(x) × H(x) + S(x)

Dimana

• F(x) : suku banyak
• H(x) : hasil bagi
• P(x) : pembagi
• S(x) : sisa

Sebelum kita memahami metode pembagian polinomial, terlebih dahulu kita harus mengetahui tentang teorema sisa yaitu

Misalkan F(x) merupakan polinomial berderajat n,

Jika F(x) dibagi (x-k) maka hasilnya adalah F(k)

Jika F(x) dibagi (ax-b) maka hasilnya adalah F(b/a)

Jika F(x) dibagi (x-a)(x-b) maka hasilnya adalah

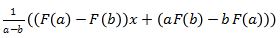
Kemudian untuk metode pembagian polinomial terdapat beberapa cara, diantaranya

1. Metode Pembagian Biasa

Contohnya adalah jika 2x3 – 3x2 + x + 5 dibagi dengan 2x2 – x – 1

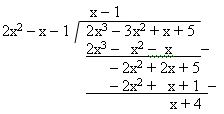
maka hasil bagi dan sisanya adalah hasil bagi = x-1 dan sisa = x+4

2. Metode Horner

Metode ini dipakai untuk pembagi yang berderajat 1 ataupun pembagi berderajat n yang bisa difaktorkan jadi pembagi-pembagi dengan derajat 1.

Langkah langkah :

1) Tulis koefisien dari polinomialnya → harus urut dari koefisien xn, xn – 1, … hingga konstanta (untuk variabel yang tidak memiliki koefisien, maka ditulis 0). Misalkan untuk 5x3 – 8, koefisien-koefisiennya adalah 5, 0, 0, dan -8

2) Untuk koefisien dengan derajat tertinggi P(x) ≠ 1, hasil baginya harus dibagi dengan koefisien derajat tertinggi P(x)

3) Jika pembagi dapat difaktorkan menjadi

• P1 dan P2, maka S(x) = P1 × S2 + S1
• P1, P2, P3, maka S(x) = P1×P2×S3 + P1×S2 + S1
• P1, P2, P3, P4, maka S(x) = P1×P2×P3×S4 + P1×P2×S3 + P1×S2 + S1
• dan seterusnya

Untuk lebih jelasnya, mari simak contoh berikut ini

Misalkan diketahui

F(x) = 2x3 – 3x2 + x + 5

P(x) =  2x2 – x – 1

Tentukan hasil bagi dan sisanya

Jawab :

F(x) = 2x3 – 3x2 + x + 5

P(x) =  2x2 – x – 1 = (2x + 1)(x – 1)

Sehingga p1 : (2x + 1) = 0 -> x = -1/2 dan p2 : (x – 1) = 0 -> x = 1

Kemudian langkah hornernya ditunjukkan pada gambar berikut

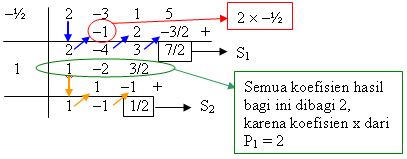
Jadi, diperoleh hasil dan sisanya sebagai berikut

H(x) = x-1

S(x) = P1×S2 + S1 = x + 4

3. Metode Koefisien Tak Tentu

Pada dasarnya, metode ini dikerjakan dengan cara mensubstitusikan F(x) berderajat m dan P(x) berderajat n ke dalam bentuk umum pembagian polinomial, kemudian H(x) dan S(x) nya diisi dengan

H(x) merupakan polinomial berderajat k, dimana k = m – n

S(x) merupakan polinomial berderajat n-k

Fungsi Pangkat

Fungsi yang memiliki bentuk 𝑓𝑥 = 𝑥^𝑎, dimana 𝑎 konstanta

disebut sebagai fungsi pangkat.

Beberapa kasus fungsi ini adalah sebagai berikut.

1. 𝑎 = 𝑛 dimana 𝑛 bilangan bulat positif.

2. 𝑎 = 1⁄𝑛 dimana 𝑛 bilangan bulat positif.

3. 𝑎 = −1.

Fungsi f pada R yang ditentukan oleh: f(x) = ax2 + bx + c dengan a, b, dan c bilangan real dan disebut fungsi kuadrat.

Jika f(x) = 0 maka diperoleh persamaan kuadrat  ax2 + bx + c = 0. Nilai-nilai x yang memenuhi persamaan itu disebut nilai pembuat nol fungsi f.

Nilai fungsi f untuk x = p ditulis f(p) = ap2 + bp + c.

Contoh :

Ditentukan: f(x) = x2 – 6x – 7

Ditanyakan:

1. nilai pembuat nol fungsi f
2. nilai f untuk x = 0 , x = –2

Jawab:

1. Nilai pembuat nol fungsi f diperoleh jika f(x) = 0

x2 – 6 x – 7 = 0

(x – 7) (x + 1) = 0

x = 7  atau  x = –1

Jadi pembuat nol fungsi f adalah 7  dan –1

2. Untuk  x = 0   maka f(0) = –7

x = –2  maka f(–2) = (–2)2 – 6 (–2) – 7 = 9

Fungsi Rasional

dimana 𝑃 dan 𝑄 adalah polinomial.

Domain fungsi ini memuat semua nilai 𝑥 sedemikian sehingga

𝑄(𝑥) ≠ 0.

Fungsi y = 1/x

Fungsi ini disebut juga sebagai fungsi kebalikan sebab setiap kita mengambil sembarang x (kecuali nol) maka akan menghasilkan kebalikannya sebagai nilai dari fungsi tersebut.

Yang artinya x yang besar akan menghasilkan nilai fungsi yang kecil, begitu juga sebaliknya. Tabel dan grafik dari fungsi tersebut bisa dilihat pada gambar di bawah ini.

Tabel dan grafik di atas memunculkan beberapa hal yang menarik. Pertama, grafik tersebut lolos uji garis vertikal, artinya, setiap garis vertikal pada bidang koordinat Cartesius memotong grafik pada maksimal satu titik. Sehingga, y = 1/x merupakan suatu fungsi. Kedua, karena pembagian tidak terdefinisi ketika pembaginya nol, maka nol tidak memiliki pasangan, yang menghasilkan jeda pada x = 0. Hal ini sesuai dengan domain dari fungsi tersebut, yaitu semua x anggota bilangan real kecuali 0. Ketiga, fungsi tersebut merupakan fungsi ganjil, dengan salah satu cabangnya berada di kuadran I sedangkan yang lainnya berada di kuadran III. Dan yang terakhir, pada kuadran I, ketika x menuju tak hingga, nilai y menuju dan mendekati nilai nol. Secara simbolis dapat ditulis sebagai x → ∞, y → 0. Secara grafis, kurva dari grafik fungsi tersebut akan mendekati sumbu-x ketika x mendekati tak hingga.

Selain itu kita juga dapat mengamati bahwa ketika x mendekati nol dari kanan maka nilai y akan mendekati bilangan real positif yang sangat besar (positif tak hingga): x → 0+, y → ∞. Sebagai catatan, tanda + atau – yang terletak di atas mengindikasikan arah dari pendekatan, yaitu dari sisi positif (+) atau dari sisi negatif (–).

---

Contoh 1: Mendeskripsikan Sifat dari Ujung Grafik Fungsi Rasional

Untuk y = 1/x dalam kuadran III,

1. Deskripsikan sifat dari ujung grafik fungsi tersebut.
2. Deskripsikan apa yang terjadi ketika x mendekati nol.

Pembahasan Serupa dengan sifat grafiknya pada kuadran I, kita mendapatkan

1. Ketika x mendekati negatif tak hingga, nilai y akan mendekati nol. Apabila disimbolkan x → –∞, y → 0.
2. Ketika x mendekati nol dari kiri, nilai y akan mendekati negatif tak hingga. Pernyataan tersebut juga dapat dituliskan dengan x → 0–, y → –∞.

---

Fungsi y = 1/x²

Dari pembahasan sebelumnya, kita dapat menduga bahwa grafik dari fungsi ini akan jeda ketika x = 0. Akan tetapi karena kuadrat dari sembarang bilangan negatif adalah bilangan positif, cabang-cabang dari grafik fungsi ini akan berada di atas sumbu-x. Perhatikan bahwa fungsi y = 1/x² merupakan fungsi genap.

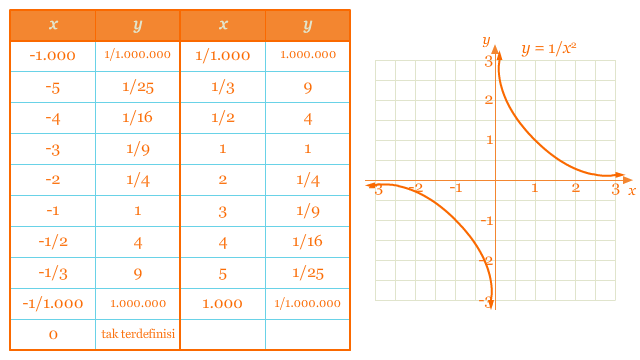
Serupa dengan y = 1/x, nilai x yang mendekati positif tak hingga, menghasilkan y yang mendekati nol: x → ∞, y → 0. Hal ini merupakan salah satu indikasi dari sifat asimtot dalam arah horizontal, dan kita mengatakan y = 0 merupakan asimtot horizontal dari fungsi y = 1/x dan y = 1/x². Secara umum,

Asimtot Horizontal
Diberikan suatu konstanta k, garis y = k merupakan asimtot horizontal dari fungsi V(x) jika x bertambah tanpa batas, menyebabkan V(x) mendekati k: x → –∞, V(x) → k atau x → ∞, V(x) → k.

Pada gambar (a) di bawah ini menunjukkan garis asimtot horizontal pada y = 1, yang menggambarkan grafik f(x) sebagai translasi grafik y = 1/x ke atas sejauh 1 satuan. Gambar (b) menunjukkan garis asimtot horizontal pada y = –2, yang menggambarkan grafik g(x) sebagai pergeseran grafik y = 1/x² ke bawah sejauh 2 satuan.

---

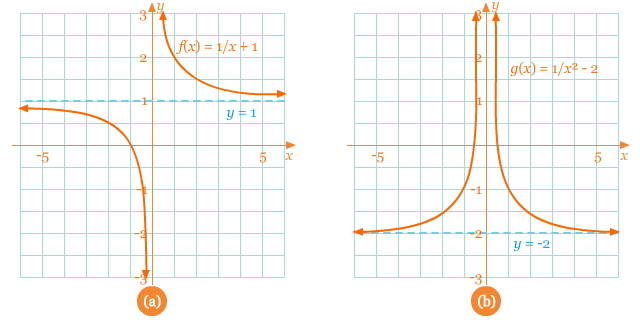
Contoh 2: Mendeskripsikan Sifat dari Ujung Grafik Fungsi Rasional

Berdasarkan gambar (b) di atas, gunakan notasi matematika untuk,

1. Mendeskripsikan sifat dari ujung grafik tersebut.
2. Mendeskripsikan apa yang terjadi ketika x mendekati nol.

Pembahasan

1. Ketika x → –∞, g(x) → –2. Ketika x → ∞, y → –2.
2. Ketika x → 0–, g(x) → ∞. Ketika x → 0+, y → ∞.

---

Dari contoh 2b di atas, kita dapat melihat bahwa ketika x mendekati nol, g menjadi sangat besar dan semakin bertambah tak terbatas. Hal ini merupakan indikasi dari sifat asimtot dalam arah vertikal, dan selanjutnya kita menyebut garis x = 0 merupakan asimtot vertikal untuk g (x = 0 juga merupakan asimtot vertikal untuk f). Secara umum,

Asimtot Vertikal
Diberikan suatu konstanta h, garis x = h merupakan asimtot vertikal untuk fungsi V jika x mendekati h, V(x) akan bertambah atau berkurang tanpa batas: ketika x → h+, V(x) → ±∞ atau ketika x → h–, V(x) → ±∞.

Mengidentifikasi dari asimtot horizontal dan vertikal sangatlah berguna karena grafik y = 1/x dan y = 1/x² dapat ditransformasi dengan menggesernya ke arah vertikal ataupun gorizontal. Fungsi,

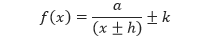
merupakan bentuk pergeseran dari fungsi y = 1/x. Sedangkan fungsi,

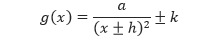
merupakan bentuk pergeseran dari fungsi y = 1/x². Selanjutnya perhatikan contoh berikut.

---

Contoh 3: Menuliskan Persamaan dari Fungsi Rasional

Identifikasi fungsi yang diberikan oleh grafik pada gambar di bawah, kemudian gunakan grafik tersebut untuk menuliskan persamaan fungsi tersebut. Anggap |a| = 1.

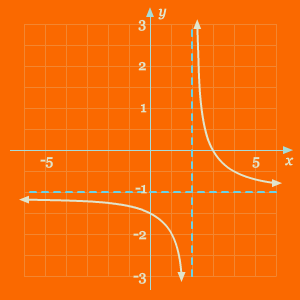
Pembahasan Dari grafik di atas, kita dapat melihat bahwa grafik tersebut merupakan pergeseran dari fungsi y = 1/x ke kanan sejauh 2 satuan dan ke bawah sejauh 1 satuan. Sehingga asimtot horizontal dan vertikal dari grafik tersebut secara berturut-turut adalah y = –1 dan x = 2. Sehingga, persamaan dari grafik di atas adalah

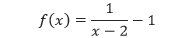
Fungsi Aljabar

Suatu fungsi 𝑓 disebut sebagai fungsi aljabar jika fungsi tersebut

dapat dibentuk dengan operasi-operasi aljabar yang dimulai dari

polinomial.

Contoh:

Fungsi Trigonometri

Definisi Sudut dan Ukuran Sudut

Sudut adalah suatu bangun yang dibentuk oleh suatu titik pangkal tertentu dan dua sinar dengan titik pangkal yang sama. Tempat titik pangkal yang merupakan pertemuan dua sinar disebut titik sudut. Sedangkan dua sinar tersebut dinamakan kaki sudut. Untuk lebih jelasnya perhatikan gambar berikut.

Fungsi Trigonometri

Fungsi trigonometri meliputi fungsi sinus, cosinus, tangen, dan fungsi kebalikan dari ketiga fungsi tersebut. Persamaan fungsi trigonometri dapat dilihat seperti penjelasan di bawah.

 
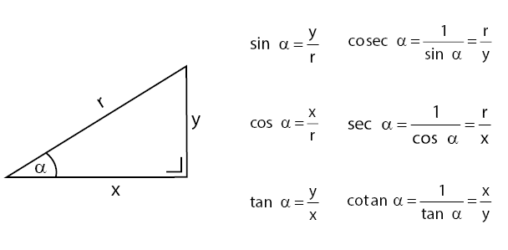
Cara untuk mengingat fungsi trigonometri dapat dilakukan dengan Jembatan Keledai: SinDeMi CosSaMi TanDeSa.
Perhatikan gambar segitiga berikut!
 

 

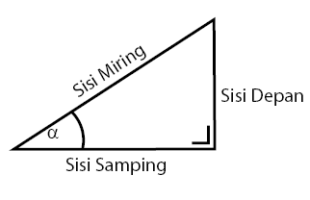
1. SinDeMi: Sinus Depan Miring

     

2. CosSaMi: Cosinus Samping Miring

     

3. TanDeSa: Tangen Depan Samping

     

 

Sudut Istimewa pada Trigonometri

Sebelum membahas mengenai sudut istimewa pada trigonometri dan nilainya, perhatikan dulu pembagian daerah diagram kartesius berikut.

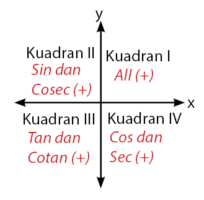
Pembagian diagram kartesius dalam empat kuadran dapat mempermudah sobat untuk menentukan nilai fungsi trigonometri. Pada kuadran I semua nilai (sin, cos, tan, dan kebalikannya) bernilai positif. Fungsi trigonometri pada kuadran II yang bernilai positif hanya sin dan kebalikannya (cosec). Pada kuadran III, fungsi trigonometri yang bernilai postif hanya tan dan kebalikannya (cotan). Sedangkan pada kuadran IV, fungsi trigonometri yang bernilai positif hanya cos dan sec. Sobat idschool hanya perlu menghafal nilai fungsi sinus untuk sudut istimewa , , , dan . Nilai sudut istimewa lainnya akan mengikuti sesuai rumus pada fungsi identitas trigonometri yang akan diberikan di bawah.

Fungsi identitas trigonometri:
Sudut 

  

  

 
Sudut 

  

  

 
Sudut 

  

  

 
Sudut 

  

  

 
Sudut 

  

  

 
Sudut 

  

  

 
Sudut 

  

  

 
Sudut 

  

 
Contoh: Cari tahu nilai dari sin !
Pembahasan:
Pilih salah satu rumus fungsi identitas trigonometri!
Misalkan saya pilih

  

Selanjutnya,

  

  

Sudut  berada pada kuadran IV. Fungsi cosinus pada kuadran IV adalah positif. Nilai . Hal ini sesuai dengan pernyataan sebelumnya, bukan?

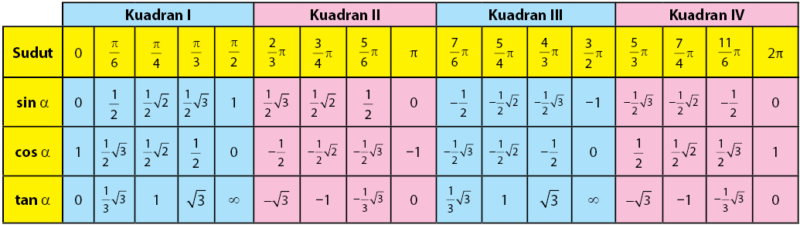
Berikut ini adalah tabel nilai fungsi trigonometri untuk sudut-sudut istimewa

Nilai sudut istimewa dalam derajat:

 
Nilai sudut istimewa dalam radian :

Fungsi Eksponensial

Pada pembahasan ini kita akan mempelajari fungsi eksponensial. Misalnya,

merupakan fungsi eksponensial yang memiliki basis 2. Perhatikan bahwa fungsi ini naik/bertambah dengan sangat cepat.

Jika kita bandingkan fungsi ini dengan fungsi g(x) = x² yang menghasilkan g(30) = 900, kita dapat melihat bahwa jika variabel fungsi berada dalam eksponen, maka perubahan kecil pada variabel akan menyebabkan perubahan yang dramatis dalam nilai fungsi.

Fungsi Eksponensial

Untuk mempelajari fungsi eksponensial, pertama kita harus mendefinisikan apa yang dimaksud dengan bentuk eksponensial ax dengan x adalah sebarang bilangan real. Dalam pembahasan ini kita sudah tahu definisi ax untuk a > 0 dan x adalah bilangan rasional, yaitu

Akan tetapi bagaimana jika x adalah bilangan irasional? Berapakah nilai dari 5√3 atau 2π? Untuk mendefinisikan ax ketika x adalah bilangan irasional, kita dekati x dengan menggunakan bilangan rasional.

Misalkan, karena

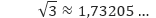
merupakan bilangan irasional, kita dapat mendekati a√3 dengan barisan pangkat bilangan rasional berikut:

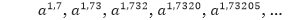
Secara intuitif, kita dapat melihat bahwa pangkat rasional dari a akan mendekat dan terus mendekat ke a√3. Dapat ditunjukkan dengan menggunakan matematika lanjut bahwa terdapat tepat satu bilangan yang didekati oleh barisan tersebut. Kita definisikan a√3 sebagai bilangan ini.

Misalkan, dengan menggunakan kalkulator, kita dapat menghitung

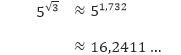
Semakin banyak desimal yang kita gunakan untuk menentukan √3 dalam perhitungan, maka kita akan mendapatkan pendekatan yang semakin baik.

---

Definisi Fungsi Eksponensial

Fungsi eksponensial f dengan basis a dinotasikan dengan

di mana a > 0, a ≠ 1, dan x merupakan sebarang bilangan real.

---

Kita menganggap bahwa a ≠ 1 karena fungsi f(x) = 1x = 1 merupakan fungsi konstan. Berikut ini beberapa contoh fungsi eksponensial:

Contoh : Menentukan Nilai Fungsi Eksponensial

Gunakan kalkulator untuk menentukan nilai masing-masing fungsi berikut pada x yang diberikan.

1. f(x) = 2x pada x = –3,1
2. f(x) = 2–x pada x = π
3. f(x) = 0,6x pada x = 3/2.

Pembahasan

1. f(–3,1) = 2–3,1 ≈ 0,1166291
2. f(π) = 2–π ≈ 0,1133147
3. f(3/2) = (0,6)3/2 = 0,4647580

Ketika menghitung nilai fungsi eksponensial dengan menggunakan kalkulator, selalu ingat untuk menutup eksponen yang berbentuk pecahan dalam tanda kurung. Hal ini dikarenakan kalkulator mengikuti urutan operasi, dan tanda kurung sangat penting untuk mendapatkan hasil yang benar.

Fungsi Logaritma

Logaritma muncul dari pertanyaan yang muncul pada operasi aritmetika dasar, yaitu perpangkatan. Misalkan diberikan perpangkatan 3 dari bilangan 4 dengan

43=64$$4^3=64$$

yang didefinisikan dengan 4×4×4=64$4\times 4\times 4=64$.

Pertanyaan balikan (baca: invers) yang berkaitan dengan fakta pangkat tersebut adalah

"4 pangkat berapa yang menghasilkan 64? ".

Maka muncul istilah logaritma dalam kasus ini, yaitu logaritma (dengan basis 4) dari 8 adalah 3.

Pada tulisan ini Anda akan disajikan teori tentang logaritma yang komperhensif. Mulai dari definisi logaritma, sifat-sifat yang dimiliki logaritma, fungsi logaritma, persamaan dan pertidak samaan logaritma dibahas pada tulisan ini.

Jangan Lewatkan : Bilangan Berpangkat

Definisi Logaritma

Seperti yang saya katakan sebelumnya dipengantar bahwa logaritma merupakan invers dari operasi perpangkatan. Secara formal definisi logaritma adalah sebagai berikut

dengan

• Bilangan  a disebut basis atau bilangan pokok
• Bilangan b disebut numerus atau domain logaritma.
• Bilangan c disebut range atau hasil logaritma.

Beberapa notasi lain yang digunakan di antaranya adalah

logab=c$${\log }_{a}b=c$$

yang berbeda peletakkan bilangan basis a$a$.

Contoh Soal 1

Nilai dari logaritma log216=4${\log }_{2}16=4$ karena 24=16$2^4=16$ dan nilai logaritma log218=−3$lo{g}_2\frac{1}{8}=-3$ karena 2−3=18$2^{-3}=\frac{1}{8}$.

Sedangkan untuk sebarang nilai basis a$a$ berlaku

logaaloga1==10$$\begin{array}{rcl}{\log }_{a}a& =& 1\\ {\log }_{a}1& =& 0\end{array}$$

karena a1=a$a^1=a$ dan a0=1$a^0=1$.

Sifat-Sifat Logaritma

Logaritma memiliki beberapa sifat yang dimiliki. Sifat ini dapat diturnkan dari definisi logaritma di atas. Biasanya sifat logaritma yang diberikan menunjukkan logaritma dari operasi suatu bilangan.

1. Sifat Penjumlahan;
   logabc=logab+logac$${\log }_{a}bc={\log }_{a}b+{\log }_{a}c$$
2. Sifat Pengurangan;
   logabc=logab−logac$${\log }_a\frac{b}{c}={\log }_{a}b-{\log }_{a}c$$
3. Sifat Perpangkatan;
   logabm=mlogab$${\log }_a{b}^m=m{\log }_{a}b$$
4. Sifat Perpangkatan 2 ;
   loganbm=mnlogab$${\log }_{a^n}{b}^m=\frac{m}{n}{\log }_{a}b$$
5. Sifat Perpangkatan 3 ;
   logab=logpblogpa$${\log }_{a}b=\frac{{\log }_{p}b}{{\log }_{p}a}$$
6. Sifat Pembagian ;
   logab=1logba$${\log }_{a}b=\frac{1}{{\log }_{b}a}$$
7. Sifat Pangkat;
   alogab=b$$a^{{\log }_{a}b}=b$$
8. Sifat Transitif;
   logad=logab⋅logbc⋅logcd$${\log }_{a}d={\log }_{a}b\cdot {\log }_{b}c\cdot {\log }_{c}d$$

Contoh Soal 2

log2(162)16log1632log232−−√===log216−log22=4−1=3=log2832log2(25)2=log225/2=52$$\begin{array}{rcl}{\log }_2\left(\frac{16}{2}\right)& =& {\log }_{2}16-{\log }_{2}2=4-1=3={\log }_{2}8\\ {16}^{{\log }_{16}32}& =& 32\\ {\log }_2\sqrt{32}& =& {\log }_2{\left(2^5\right)}^2={\log }_2{2}^{5/2}=\frac{5}{2}\end{array}$$

Baca Juga : Logaritma dengan Bilangan Pokok e

Fungsi Logaritma

Seperti halnya yang lain, fungsi logaritma mempunyai domain dan range. Definisi bentuk logaritma berasal dari operasi pangkat sehingga fungsi logaritma pun pendefinisian sama dengan definisi logaritma tersebut.

DEFINISI

Misalkan g:R→R$g:\mathbb{R}\to \mathbb{R}$ yang didefinisikan

g(x):=ax$$g(x):=a^x$$

dengan a>0,a≠1$a>0,a\ne 1$. Invers fungsi g$g$ adalah fungsi logaritmag−1=f$g^{-1}=f$ didefinisikan dengan

f(x)=logax$$\mathit{f}\mathbf{(}\mathit{x}\mathbf{)}\mathbf{=}{\mathbf{log}}_{\mathit{a}}\mathit{x}$$

Jika fungsi logaritma f(x)=logx$f(x)=\log x$ akan terlihat seperti di bawah ini

Untuk lebih memperjelas, silahkan Anda lihat grafik fungsi logaritma di bawah ini

Gambar di atas menunjukan grafik fungsi g(x)=10x$g(x)={10}^x$ dan grafik inversnya, yaitu fungsi logaritma f(x)=log10(x)$f(x)={\log }_{10}(x)$.

Mari kita lihat beberapa grafik dari fungsi logaritma lainnya dengan bilangan basis selain 10.

Waaahh...grafiknya keren kan. Apa yang Anda tangkap dari grafik di atas.

Mari kita lihat satu persatu

Titik potong grafik fungsi logaritma terhadap sumbu-X$X$ adalah titik (1,0)$(1,0)$. Karena jika Anda subtitusi f(x)=y=0$f(x)=y=0$ maka diperoleh

f(x)0x===loga(x)loga(x)1$$\begin{array}{rcl}f(x)& =& {\log }_a(x)\\ 0& =& {\log }_a(x)\\ x& =& 1\end{array}$$

Satu tanda berikutnya adalah jika bilangan basisnya a>1$a>1$ maka fungsi logaritma f(x)=loga(x)$f(x)={\log }_a(x)$ adalah fungsi naik. Sedangkan fungsi logaritma f(x)=loga(x)$f(x)={\log }_a(x)$ turun jika nilai basisnya 0<a<1$0<a<1$.

Contoh Soal 3
Perhatikan gambar dibawah. Jika f(x)=log2(x)$f(x)={\log }_2(x)$ maka fungsi yang dinyatakan grafik berwarna merah adalah ...

Pembahasan Contoh Soal 3
Grafik dengan warna merah adalah translasi grafik fungsi logaritma (warna hitam) f(x)=log2(x)$f(x)={\log }_2(x)$ ke arah kiri 2 satuan. Jadi persamaan yang dimaksud adalah fungsi logaritma g(x)=log2(x+2)$g(x)={\log }_2(x+2)$.
Lebih lanjut untuk x=−1$x=-1$ maka y=log2(−1+2)=0$y={\log }_2(-1+2)=0$. Jadi titik (−1,0)$(-1,0)$ berada pada grafik fungsi logaritma y=log2(x+2)$y={\log }_2(x+2)$ atau dengan kata lain titik potong sumbu-x$x$ adalah (−1,0)$(-1,0)$


Contoh Soal 4
Fungsi y=log1/2(x)$y={\log }_{1/2}(x)$ berada di atas sumbu-x$x$ ketika ...

Pembahasan Contoh Soal 4
Berdasarkan sifat yang kita sebut di atas, maka dapat disimpulkan grafik fungsi y=log12(x)$y={\log }_{\frac{1}{2}}(x)$ berada di atas sumbu-x$x$ ketika

0<x<1$$0<x<1$$

memotong sumbu-x$x$ di x=1$x=1$ dan melewati (12,1)$\left(\frac{1}{2},1\right)$ dan dibawah sumbu-x$x$ jika

x>1$$x>1$$

Perhatikan grafik fungsi y=log12(x)$y={\log }_{\frac{1}{2}}(x)$ berikut

Persamaan Logaritma

Persamaan logaritma merupakan persamaan yang memuat bentuk logaritma, baik variabel x$x$ sebagai tanda logaritma maupun variabel x$x$ sebagai bilangan pokok atau bilangan basis suatu logaritma.

Jika suatu persamaan memuat bentuk logaritma maka ada beberapa sifat yang berlaku pada persamaan logaritma.

1. Jika logaf(x)=logap${\log }_{a}f(x)={\log }_{a}p$, maka f(x)=p$f(x)=p$ asalkan f(x)>0$f(x)>0$
2. Jika logaf(x)=logbf(x)${\log }_{a}f(x)={\log }_{b}f(x)$, dengan a≠b$a\ne b$ maka f(x)=1$f(x)=1$
3. Jika logaf(x)=logag(x)${\log }_{a}f(x)={\log }_{a}g(x)$, maka f(x)=g(x)$f(x)=g(x)$ asalkan f(x)>0$f(x)>0$ dan g(x)>0$g(x)>0$
4. Jika logh(x)f(x)=logh(x)g(x)${\log }_{h(x)}f(x)={\log }_{h(x)}g(x)$, maka f(x)=g(x)$f(x)=g(x)$ asalkan f(x)>0,g(x)>0$f(x)>0,g(x)>0$ serta h(x)>0$h(x)>0$ dan h(x)≠1$h(x)\ne 1$
5. Jika logf(x)h(x)=logg(x)h(x)${\log }_{f(x)}h(x)={\log }_{g(x)}h(x)$, maka beberapa kemungkinan adalah
   1. f(x)=g(x)$f(x)=g(x)$ dengan syarat h(x)=1,f(x)>0,f(x)≠1,g(x)>0,g(x)≠1$h(x)=1,f(x)>0,f(x)\ne 1,g(x)>0,g(x)\ne 1$
   2. f(x)=g(x)$f(x)=g(x)$ dengan syarat h(x)≠1,h(x)>0$h(x)\ne 1,h(x)>0$

Contoh Soal 5
Nilai x$x$ yang memenuhi persamaan log3x+227=log53${\log }_{3x+2}27={\log }_{5}3$ adalah...

Pembahasan Contoh Soal 5
Berdasarkan sifat-sifat persamaan logaritma diperoleh

log3x+227log3x+2333x+23x+23xx======log53log53335312512341$$\begin{array}{rcl}{\log }_{3x+2}27& =& {\log }_{5}3\\ {\log }_{3x+2}{3}^3& =& {\log }_{5^3}{3}^3\\ 3x+2& =& 5^3\\ 3x+2& =& 125\\ 3x& =& 123\\ x& =& 41\end{array}$$

Contoh Soal 6
Jika diketahui log98=3m${\log }_{9}8=3m$ maka nilai log43=⋯${\log }_{4}3=\cdots$

Pembahasan Contoh Soal 5
Berdasarkan sifat persamaan logaritma di atas

log98log8log9log23log323log2log2x======3m3m3m3m⋅2log32mlog341$$\begin{array}{rcl}{\log }_{9}8& =& 3m\\ \frac{\log 8}{\log 9}& =& 3m\\ \frac{\log 2^3}{\log 3^2}& =& 3m\\ 3\log 2& =& 3m\cdot 2\log 3\\ \log 2& =& 2m\log 3\\ x& =& 41\end{array}$$

Selanjutnya dapat dicari nilai yang dimaksud

log43====log3log4log32log2log32⋅2log314m$$\begin{array}{rcl}{\log }_{4}3& =& \frac{\log 3}{\log 4}\\ & =& \frac{\log 3}{2\log 2}\\ & =& \frac{\log 3}{2\cdot 2\log 3}\\ & =& \frac{1}{4m}\end{array}$$

Pertidaksamaan Logaritma

Pertidaksamaan logaritma adalah pertidaksamaan yang mengandung fungsi-fungsi logaritma dengan bentuk umum

logaf(x)>logag(x)$${\log }_{a}f(x)>{\log }_{a}g(x)$$

yang menunjukkan bahwa

f(x)>g(x),f(x)<g(x),      a>10<a<1$$\begin{array}{rcl}f(x)>g(x),& & a>1\\ f(x)<g(x),& & 0<a<1\end{array}$$

Oleh karena itu untuk menyelesaikan pertidaksamaan logaritma tersebut digunakan langkah-langkah berikut

Pertama dicek syarat-syarat f(x)>0$f(x)>0$ dan g(x)>0$g(x)>0$. Selanjutnya diselesaikan pertidaksamaan f(x)>g(x)$f(x)>g(x)$ untuk a>1$a>1$ dan f(x)<g(x)$f(x)<g(x)$ untuk 0<a<1$0<a<1$

Contoh Soal 6

Nilai x$x$ yang memenuhi pertidaksamaan logaritma berikut adalah

log2(2x+7)>2$${\log }_2(2x+7)>2$$

Pembahasan Contoh Soal 6

Akan kita cek syarat pertama yaitu

2x+72xx>>>0−7−72                   ⋯(⋆)$$\begin{array}{rcl}2x+7& >& 0\\ 2x& >& -7\\ x& >& -\frac{7}{2}\cdots (\star )\end{array}$$

Selanjutnya diselesaikan pertidaksamaan logaritma yang dimaksud

log2(2x+7)log2(2x+7)2x+72xx>>>>>2log222224−7−32                   ⋯(⋆⋆)$$\begin{array}{rcl}{\log }_2(2x+7)& >& 2\\ {\log }_2(2x+7)& >& {\log }_2{2}^2\\ 2x+7& >& 2^2\\ 2x& >& 4-7\\ x& >& -\frac{3}{2}\cdots (\star \star )\end{array}$$

Berdasarkan (⋆)$(\star )$ dan (⋆⋆)$(\star \star )$ diperoleh himpunan penyelesaian {x∈R:x>−32}

Fungsi logaritma 𝑓𝑥 = log𝑏𝑥, dimana basis 𝑏 merupakan

konstanta positif, adalah fungsi invers dari fungsi eksponensial.

untuk lebih jelasnya bisa dilihat di video dibawah ini

Sumber Referensi : Artikel Blog Education