Aplikasi Integral
Menentukan Panjang Busur
Assalamu'alaikum Wr. Wb
Hari ini saya akan menjelaskan materi tentang menentukan panjang busur dengan metode integral
nah, apakah kalian sudah pernah mendengar materi ini ???
jika belum, kita langsung saja membahasa tentang materi ini. lets go.....
Panjang suatu busur dapat ditentukan dengan menggunakan integral tentu. Suatu busur (ruas dari suatu kurva) dapat didekati dengan menggunakan ruas garis lurus yang panjangnya dapat ditentukan dengan menggunakan rumus jarak,

Misalkan fungsi y = f(x) merupakan fungsi yang kontinu dan memiliki turunan pada interval [a, b]. Perlu diingat bahwa fungsi yang demikian memiliki f ’ yang memiliki turunan di [a, b] dan memiliki grafik berupa kurva halus. Grafik dari fungsi f tersebut dapat ditaksir dengan menggunakan ruas garis-ruas garis yang titik-titik ujungnya ditentukan oleh partisi

seperti yang ditunjukkan oleh gambar di bawah ini.

Dengan memisalkan Δx = xi – xi – 1 dan Δy = yi – yi – 1, panjang ruas dari suatu grafik dapat diperkirakan sebagai berikut.

Perkiraan tersebut akan semakin baik dan baik apabila ||Δ|| → 0 atau n → ∞. Sehingga, panjang ruas dari grafik tersebut adalah

Karena fungsi yang diberikan adalah fungsi yang memiliki turunan pada interval [a, b], maka fungsi tersebut memiliki turunan di (xi – 1, xi). Sehingga Teorema Nilai Rata-rata menjamin adanya ci di (xi – 1, xi) sedemikian sehingga,
Karena f ’ kontinu pada interval [a, b] maka √(1 + [f ’(ci)]2) juga kontinu (sehingga memiliki integral) pada [a, b], yang mengakibatkan
di mana s disebut panjang busur f antara a dan b.
DEFINISI PANJANG BUSUR
Misalkan fungsi y = f(x) memiliki kurva halus pada interval [a, b]. Panjang busur f antara a dan b adalah
Dengan cara yang sama, untuk kurva halus yang diberikan oleh x = g(y), panjang busur g antara c dan d adalah
Karena definisi dari panjang busur dapat diaplikasikan pada fungsi linear, maka definisi baru ini dapat diperiksa apakah definisi tersebut memenuhi rumus jarak ataukah tidak. Perhatikan contoh 1 berikut.
Contoh 1: Panjang dari Suatu Ruas Garis
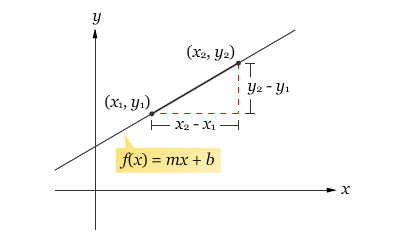
Tentukan panjang busur dari (x1, y1) ke (x2, y2) pada grafik f(x) = mx + b, seperti yang ditunjukkan oleh gambar berikut.
Pembahasan Karena

maka hal ini akan menyebabkan
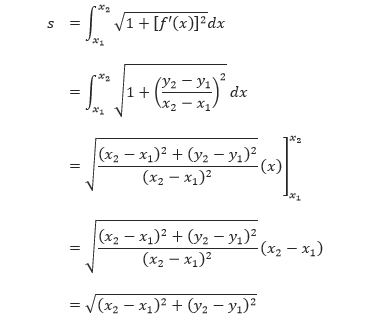
yang merupakan rumus untuk menentukan jarak antara dua titik pada bidang.
Contoh 2: Panjang dari Suatu Kabel
Suatu kabel listrik tergantung di antara dua tiang yang terpisah sejauh 200 meter, seperti yang ditunjukkan oleh gambar di bawah ini.

Kabel tersebut memiliki bentuk grafik yang persamaannya,

Tentukan panjang kabel di antara kedua tiang listrik tersebut.
Pembahasan Karena y’ = (1/2)(ex/150 – e–x/150), maka akan menghasilkan

dan

Sehingga, panjang kabel di antara dua tiang listrik tersebut adalah

untuk lebih lanjutnya materi teorema pythagoras, saksikan video dibawah ini






Tidak ada komentar:
Posting Komentar